Skip to main content

Advertisement

SpringerLink
Log in

A quasi-Gaussian approximation method for the Duffing oscillator with colored additive random excitation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

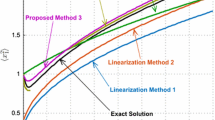
Statistical analysis of stochastic dynamical systems is of considerable importance for engineers as well as scientists. Engineering applications require approximate statistical methods with a trade-off between accuracy and simplicity. Most exact and approximate methods available in the literature to study stochastic differential equations (SDEs) are best suited for linear or lightly nonlinear systems. When a system is highly nonlinear, e.g., a system with multiple equilibria, the accuracy of conventional methods degrades. This problem is addressed in this article, and a novel method is introduced for statistical analysis of special types of essentially nonlinear SDEs. In particular, second-order dynamical systems with nonlinear stiffness and additive random excitations are considered. The proposed approximate method can estimate second-order moments of the state vector (namely position and velocity), not only in the case of white noise excitation, but also when the excitation is a correlated noise. To illustrate the efficiency, a second-order dynamical system with bistable Duffing-type nonlinearity is considered as the case study. Results of the proposed method are compared with the Gaussian moment closure approximation for two types of colored noise excitations, one with first-order dynamics and the other with second-order dynamics. In the absence of exact closed-form solutions, Monte Carlo simulations are considered as the reference ideal solution. Results indicate that the proposed method gives proper approximations for the mean square value of position, for which the Gaussian moment closure method cannot provide good estimations. On the other hand, both methods provide acceptable estimations for the mean square value of velocity in terms of accuracy. Such nonlinear SDEs especially arise in energy-harvesting applications, when the ambient vibration can be modeled as a wideband random excitation. In such conditions, linear energy harvesters are no longer optimal designs, but nonlinear broadband harvesting techniques are hoped to show much better performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Smith, R.C.: Uncertainty Quantification: Theory, Implementation, and Applications. SIAM, Bangkok (2013)

    Google Scholar 

  2. Yang, C.Y.: Random Vibration of Structures. Wiley, New York (1986)

    Google Scholar 

  3. Henderson, D., Plaschko, P.: Stochastic Differential Equations in Science and Engineering. World Scientific Publishing, Singapore (2006)

    Book  MATH  Google Scholar 

  4. Cottone, F., Vocca, H., Gammaitoni, L.: Nonlinear energy harvesting. Phys. Rev. Lett. 102(8), 80601 (2009)

    Article  Google Scholar 

  5. Briand, D., Yeatman, E., Roundy, S. (eds.): Micro Energy Harvesting, vol. XXXIII. Wiley, Weinheim (2015)

    Google Scholar 

  6. Newland, D.E.: An Introduction to Random Vibrations, Spectral and Wavelet Analysis, 3rd edn. Wiley, New York (1993)

    Google Scholar 

  7. Socha, L.: Linearization Methods for Stochastic Dynamic Systems. Springer, Berlin (2008)

    MATH  Google Scholar 

  8. Ibrahim, R.A.: Parametric Random Vibration. Wiley, New York (1985)

    MATH  Google Scholar 

  9. Socha, L.: Linearization in analysis of nonlinear stochastic systems: recent results-part I: theory. Appl. Mech. Rev. 58(3), 178 (2005)

    Article  MathSciNet  Google Scholar 

  10. Caughey, T.K.: Equivalent linearization techniques. J. Acoust. Soc. Am. 34(12), 2001–2001 (1962)

    Article  Google Scholar 

  11. Roberts, J.B., Spanos, P.D.: Random Vibration and Statistical Linearization. Courier Dover Publications, New York (2003)

    MATH  Google Scholar 

  12. Spanos, P.T.D.: Formulation of stochastic linearization for symmetric or asymmetric MDOF nonlinear systems. J. Appl. Mech. 47(1), 209 (1980)

    Article  MATH  Google Scholar 

  13. Di Paola, M., Falsone, G., Pirrotta, A., Palermo, U., Scienze, V.: Stochastic response analysis of nonlinear systems under Gaussian inputs. Probab. Eng. Mech. 7, 15–21 (1992)

    Article  Google Scholar 

  14. Sun, J., Hsu, C.S.: Cumulant-neglect closure method for nonlinear systems under random excitations. J. Appl. Mech. 54(3), 649 (1987)

    Article  MATH  Google Scholar 

  15. Wu, W.F., Lin, Y.K.: Cumulant-neglect closure for non-linear oscillators under random parametric and external excitations. Int. J. Nonlinear. Mech. 19(4), 349–362 (1984)

    Article  MATH  Google Scholar 

  16. Crandall, S.H.: Non-Gaussian closure for random vibration of non-linear oscillators. Int. J. Nonlinear. Mech. 15(4–5), 303–313 (1980)

    Article  MATH  Google Scholar 

  17. Makarem, H., Pishkenari, H.N., Vossoughi, G.R.: A modified Gaussian moment closure method for nonlinear stochastic differential equations. Nonlinear Dyn. 89(4), 2609–2620 (2017)

    Article  MathSciNet  Google Scholar 

  18. Zhu, W.Q.: Stochastic averaging methods in random vibration. Appl. Mech. Rev. 41(5), 189 (1988)

    Article  Google Scholar 

  19. Roberts, J.B., Spanos, P.D.: Stochastic averaging: an approximate method of solving random vibration problems. Int. J. Nonlinear Mech. 21(2), 111–134 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  20. Lin, Y.K.: Some observations on the stochastic averaging method. Probab. Eng. Mech. 1(1), 23–27 (1986)

    Article  Google Scholar 

  21. Zhu, B.W., Lin, Y.K.: Stochastic averaging of energy envelope. J. Eng. Mech. 117(8), 1890–1905 (1992)

    Article  Google Scholar 

  22. Di Paola, M., Sofi, A.: Approximate solution of the Fokker–Planck–Kolmogorov equation. Probab. Eng. Mech. 17, 369–384 (2002)

    Article  Google Scholar 

  23. Soize, C.: Steady-state solution of Fokker–Planck equation in higher dimension. Probab. Eng. Mech. 3(4), 196–206 (1988)

    Article  Google Scholar 

  24. Er, G.-K.: A consistent method for the solution to reduced FPK equation in statistical mechanics. Phys. A Stat. Mech. Appl. 262(1–2), 118–128 (1999)

    Article  Google Scholar 

  25. Er, G.-K., Iu, V.P.: The approximate solutions of FPK equations in high dimensions for some nonlinear stochastic dynamic systems. Commun. Comput. Phys. 10(5), 1241–1256 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. To, C.W.S.: Nonlinear Random Vibration: Analytical Techniques and Applications, 2nd edn. CRC Press, Boca Raton (2012)

    MATH  Google Scholar 

  27. Joo, H.K., Sapsis, T.P.: A moment-equation-copula-closure method for nonlinear vibrational systems subjected to correlated noise. Probab. Eng. Mech. 46, 120–132 (2016)

    Article  Google Scholar 

  28. Daqaq, M.F.: Transduction of a bistable inductive generator driven by white and exponentially correlated Gaussian noise. J. Sound Vib. 330(11), 2554–2564 (2011)

    Article  Google Scholar 

  29. Fan, F.G., Ahmadi, G.: On loss of accuracy and non-uniqueness of solutions generated by equivalent linearization and cumulant-neglect methods. J. Sound Vib. 137(3), 385–401 (1990)

    Article  MATH  Google Scholar 

  30. Daqaq, M.F.: On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations. Nonlinear Dyn. 69(3), 1063–1079 (2012)

    Article  MathSciNet  Google Scholar 

  31. Ibrahim, R.A., Soundararajan, A.: An improved approach for random parametric response of dynamic systems with non-linear inertia. Int. J. Non. Linear. Mech. 20(4), 309–323 (1985)

    Article  MATH  Google Scholar 

  32. Kumar, P., Narayanan, S., Adhikari, S., Friswell, M.I.: Fokker–Planck equation analysis of randomly excited nonlinear energy harvester. J. Sound Vib. 333(7), 2040–2053 (2014)

    Article  Google Scholar 

  33. Risken, H.: The Fokker–Planck Equation: Methods of Solution and Applications. Springer, Berlin (1989)

    Book  MATH  Google Scholar 

  34. Spencer, B.F., Bergman, L.: On the numerical solution of the Fokker–Planck equation for nonlinear stochastic systems. Nonlinear Dyn. 4, 357–372 (1993)

    Article  Google Scholar 

  35. Kovacic, I., Brennan, M.J.: The Duffing Equation: Nonlinear Oscillators and Their Behaviour. Wiley, New York (2011)

    Book  MATH  Google Scholar 

  36. Jazwinski, A.H.: Stochastic Processes and Filtering Theory. Academic Press, Cambridge (1970)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Nano Robotics Laboratory, Mechanical Engineering Department, Sharif University of Technology, Tehran, Iran

    H. N. Pishkenari

  2. Center of Excellence in Design, Robotics and Automation (CEDRA), Mechanical Engineering Department, Sharif University of Technology, Tehran, Iran

    H. Makarem, H. N. Pishkenari & G. R. Vossoughi

Authors
  1. H. Makarem
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. N. Pishkenari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. R. Vossoughi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. N. Pishkenari.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Makarem, H., Pishkenari, H.N. & Vossoughi, G.R. A quasi-Gaussian approximation method for the Duffing oscillator with colored additive random excitation. Nonlinear Dyn 96, 825–835 (2019). https://doi.org/10.1007/s11071-019-04824-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-04824-x

Keywords

Search

Navigation